Giải Toán lớp 9 SGK Tập 2 trang 20, 21, 22 (Chính xác nhất)

Giải bài tập SGK Toán lớp 9 Bài 5: Giải bài toán bằng cách lập hệ phương trình được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình SGK Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.

Giải toán 9 Bài 5: Giải bài toán bằng cách lập hệ phương trình

Trả lời câu hỏi Toán 9 Tập 2 Bài 5 trang 20:

Hãy nhắc lại những bước giải bài toán bằng cách lập phương trình .

Lời giải

Bước 1 : Lập phương trình
– Chọn ẩn số và đặt điều kiện kèm theo thích hợp cho ẩn số
– Biểu diễn những đại lượng chưa biết theo ẩn và những đại lượng đã biết
– Lập phương trình bộc lộ mối quan hệ giữa những đại lượng
Bước 2 : giải phương trình
Bước 3 : Trả lời : Kiểm tra xem trong những nghiệm của phương trình, nghiệm nào thỏa mãn nhu cầu điều kiện kèm theo của ẩn, nghiệm nào không, rồi Kết luận

Trả lời câu hỏi Toán 9 Tập 2 Bài 5 trang 21(1):

Giải hệ phương trình ( I ) và vấn đáp bài toán đã cho .

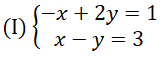
Lời giải

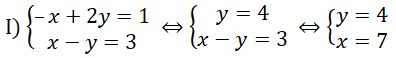
Vậy số cần tìm là 74

Trả lời câu hỏi Toán 9 Tập 2 Bài 5 trang 21 (2):

Lập phương trình biểu lộ giả thiết : Mỗi giờ, xe khách đi nhanh hơn xe tải 13 km .

Lời giải

Mỗi giờ xe khách đi nhanh hơn xe tải là 13 km nên ta có phương trình
y – x = 13 ⇔ y = 13 + x

Trả lời câu hỏi Toán 9 Tập 2 Bài 5 trang 21 (3):

Viết những biểu thức chứa ẩn biểu lộ quãng đường mỗi xe đi được, tính đến khi hai xe gặp lại nhau. Từ đó suy ra phương trình biểu lộ giả thiết quãng đường từ TP. Hồ Chí Minh đến TP. Cần Thơ dài 189 km .

Lời giải

Quãng đường xe khách đi được đến khi gặp nhau là : 9/5 y ( km )
Quãng đường xe tải đi được đến khi gặp nhau là : 14/5 x ( km )
Theo giả thiết quãng đường từ TP. Hồ Chí Minh đến TP. Cần Thơ dài 189 km nên ta có phương trình

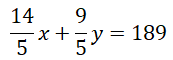
Trả lời câu hỏi Toán 9 Tập 2 Bài 5 trang 21 (4):

Giải hệ hai phương trình thu được trong câu hỏi 3 và câu hỏi 4 rồi vấn đáp bài toán .

Lời giải

Từ ? 3 và ? 4 ta có hệ phương trình

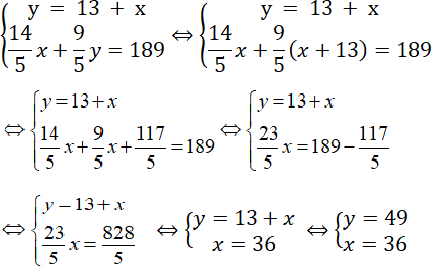
Vậy tốc độ của xe tải là 36 km / h
Vận tốc của xe khách là 49 km / h

Bài 28 (trang 22 SGK Toán 9 Tập 2):

Tìm hai số tự nhiên, biết rằng tổng của chúng bằng 1006 và nếu lấy số lớn chia cho số nhỏ thì được thương là 2 và số dư là 124 .

Lời giải

Gọi số lớn là x, số nhỏ là y ( x, y ∈ N * ) ; x, y > 124 .
Tổng hai số bằng 1006 nên ta có : x + y = 1006
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có : x = 2 y + 124 .
Ta có hệ phương trình :

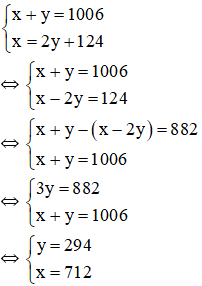
Vậy hai số tự nhiên phải tìm là 712 và 294 .
Chú ý : Số bị chia = số chia. thương + số dư

Bài 29 (trang 22 SGK Toán 9 Tập 2):

Giải bài toán cổ sau :
Quýt, cam mười bảy quả tươi
Đem chia cho một trăm người cùng vui
Chia ba mỗi quả quýt rồi
Còn cam mỗi quả chia mười vừa xinh
Trăm người, trăm miếng ngọt lành
Quýt, cam mỗi loại tính rành là bao ?

Phương pháp giải:

Giải bài toán bằng cách lập hệ phương trình :

Bước 1: Lập hệ phương trình

– Chọn những ẩn số và đặt điều kiện kèm theo thích hợp
– Biểu diễn những đại lượng chưa biết và đã biết theo ẩn
– Lập những phương trình bộc lộ mối quan hệ giữa những đại lượng theo đề bài .
– Từ những phương trình vừa lập rút ra được hệ phương trình .

Bước 2: Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).

Bước 3: Đối chiếu nghiệm với điều kiện và kết luận.

Lời giải

Gọi số cam là x, số quýt là y ( x, y ∈ N * ; x < 17, y < 17 ) .Quýt, cam 17 quả tươi ⇒ x + y = 17 .Mỗi quả quýt chia ba ⇒ Có 3 y miếng quýtChia mười mỗi quả cam ⇒ Có 10 x miếng camTổng số miếng tròn 100 ⇒ 10 x + 3 y = 100 .Ta có hệ phương trình :

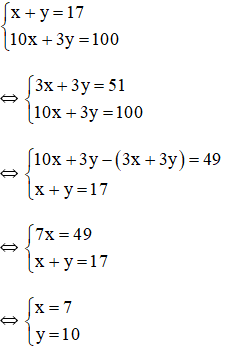
Vậy có 7 quả cam và 10 quả quýt .

Bài 30 (trang 22 SGK Toán 9 Tập 2):

Một ôtô đi từ A và dự tính đến B lức 12 giờ trưa. Nếu xe chạy với tốc độ 35 km / h thì sẽ đến B chậm 2 giờ so với dự đinh. Nếu xe chạy với tốc độ 50 km / h thì sẽ đến B sớm 1 giờ so với dự tính. Tính độ dài quãng đường AB và thời gian xuất phát của ôtô tại A .

Lời giải

Gọi x ( km ) là độ dài quãng đường AB, y ( giờ ) là thời hạn dự tính đi để đến B đúng lúc 12 giờ trưa .
Điều kiện x > 0, y > 1 ( do ôtô đến B sớm hơn 1 giờ ) .
+ Với v = 35 km / h thì thời hạn đi hết quãng đường AB là : t = X / 35 ( giờ )
Ô tô đến chậm hơn 2 giờ so với dự tính ⇒ X / 35 = Y + 2 ⇔ x = 35 y + 70 .

+ Với v = 50 km/h thì thời gian đi hết quãng đường AB là : T = X/50 (giờ)

Ô tô đến sớm hơn 1 h so với dự tính ⇒ x / 50 = y – 1 ⇔ x = 50 y – 50 .
Ngoài ra những em học viên và thầy cô hoàn toàn có thể tìm hiểu thêm thêm nhiều tài liệu có ích không thiếu những môn được update liên tục tại chuyên trang của chúng tôi .

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về hướng dẫn giải Toán lớp 9 SGK Tập 2 trang 20, 21, 22 file Word, pdf hoàn toàn miễn phí!

Source: https://mix166.vn
Category: Hỏi Đáp