ÔN TẬP TOÁN HÌNH HỌC LỚP 8 HKI - The first knowledge sharing application in Vietnam

Posted 14/11/2011 by Trần Thanh Phong in Hình học 8, Lớp 8. Tagged : ôn tập toán. 255 phản hồiN TẬP TOÁN HÌNH HỌC LỚP 8 HKI

BÀI 1 : Cho tam giác ABC cân tại A.Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC.

Bạn đang đọc: ÔN TẬP TOÁN HÌNH HỌC LỚP 8 HKI

Vẽ điểm M là điểm đối xứng của điểm B qua điểm F và điểm N là điểm đối xứng của điểm E qua điểm D. 1 ) Chứng minh :
a / Tứ giác BCFD là hình thang cân .
b / Tứ giác ADEF là hình thoi .
c / Tứ giác ABCM là hình bình hành .
d / Tứ giác ANBE là hình chữ nhật .

Mục lục bài viết

GIẢI.

a/ Tứ giác BCFD là hình thang cân.

Xét ?ABC, ta có :
DA = DB ( gt )
FA = FC ( gt )
=> DF là đường trung bình trong ?ABC .
=> DF / / BC
=> Tứ giác BCFD là hình thang

Mà : $\widehat{ABC} =\widehat{ACB}$ (?ABC cân tại A)

=> hình thang BCFD là hình thang cân .

b / Tứ giác ADEF là hình thoi :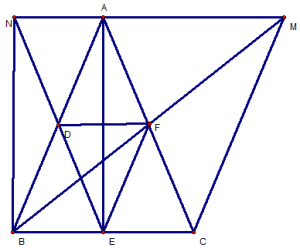

Ta có :
AB = AC ( gt )
AD = AB : 2 ( gt )
AF = AC : 2 ( gt )
=> AD = AF = AC : 2 = AB : 2 ( 1 )
Xét ΔABC, ta có :
DA = DB ( gt )
EB = EC ( gt )
=> DE là đường trung bình
=> DE = AC : 2 ( 2 )
Cmtt, ta được : EF = BA : 2 ( 3 )
Từ ( 1 ), ( 2 ) và ( 3 ) ta được : AD = AF = DE = EF
Vậy tứ giác ADEF là hình thoi .

c/ Tứ giác ABCM là hình bình hành :

Xét Tứ giác ABCM, ta có :
FB = FM ( M là điểm đối xứng của điểm B qua điểm F )
FA = FC ( gt )
Mà hai đường chéo BM và AC cắt nhau tại F .
=> Tứ giác ABCM là hình bình hành .

d/ Tứ giác ANBE là hình chữ nhật :

Xét ΔABC cân tại A, ta có :
EB = EC ( gt )
=> AE là đường trung tuyến trong tam giác cân cũng là đường cao .

=> AE $\bot$ BC hay $\widehat{AEB} =90^0$

Xét Tứ giác ANBE, ta có :
Xét Tứ giác ABCM, ta có :
DE = DN ( N là điểm đối xứng của điểm E qua điểm D )
DA = DB ( gt )
Mà hai đường chéo EN và AB cắt nhau tại D .
=> Tứ giác ANBE là hình bình hành .
Mà : ( cmt )
Nên : hình bình hành ANBE là hình chữ nhật .

— — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — —

BÀI 2 :

Cho hình thang cân ABCD ( AB / / CD ). Gọi M, N, P, Q. lần lượt là trung điểm của AB, BC, CD, DA .
a / Chứng minh : Tứ giác MNPQ làhình bình hành .
b / Chứng minh : Tứ giác MNPQ làhình thoi .
c / Nếu AC BD thì tứ giác MNPQ là hình gì ? Vì sao ?

Giải

Tứ giác MNPQ làhình bình hành :

Xét ABD, ta có :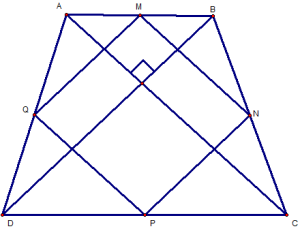

MA = MB ( gt )
QA = QD ( gt )
=> MQ là đường trung bình .
=> MQ / / BD và MQ = BD : 2 ( 1 )
Cmtt, ta được :
NP / / BD và NP = BD : 2 ( 2 )
NM / / AC và NM = AC : 2 ( 3 )
Từ ( 1 ) và ( 2 ) : MQ / / NP và MQ = PP
=> Tứ giác MNPQ làhình bình hành .

b/Tứ giác MNPQ làhình thoi.

ta có :
AC = BD ( hai đường chéo hình thang cân ABCD )
NM = AC : 2 ( cmt )
MQ = BD : 2 ( cmt )
=> NM = MQ
Xét hình bình hành MNPQ, ta có :
NM = MQ ( cmt )
=> hình bình hành MNPQ là hình thoi .
c / Nếu AC BD thì tứ giác MNPQ là hình gì ?
Nếu AC BD
NM / / AC ( cmt )
NP / / BD ( cmt )
=> NM NP tại N

Hay $\widehat{MNP} =90^0$

Xét hình thoi MNPQ, ta có : ( cmt )

=> hình thoi MNPQ là hình vuông.

Xem thêm: Tết Thanh minh năm 2022 là ngày nào dương lịch và âm lịch

— — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — –

BÀI 3 :

Cho tam giác ABC vuông tại A ( AB > AC ), đường trung tuyến AO. Trên tia đối của tia OA lấy điểm D sao cho OD = OA .

Chứng minh : ABDC là hình chữ nhật.
Từ B kẻ BH vuông góc AD tại H, Từ C kẻ CK vuông góc AD tại K. chứng minh BH = CK và BK // CH.
Tia BH cắt CD ở M, tia CK cắt AB ở K. chứng minh ba điểm M, O, N thẳng hàng.
Trên tia đối của tia BH lấy điểm E sao cho BE = AD. Chứng minh $\widehat{DCE}=45^0$

GIẢI.

1. ABDC là hình chữ nhật :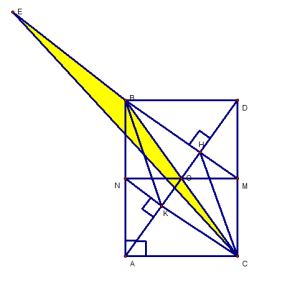

Xét tứ giác ABDC, ta có :
OB = OC ( đường trung tuyến AO của ?ABC )
OA = OD ( gt )
=> tứ giác ABDC là hình bình hành

Mà : $\widehat{}=90^0$ (gt)

=> hình bình hành ABDC là hình chữ nhật

2. BH = CK và BK // CH :

Xét ?HOB và ?OC, ta có :

$\widehat{BHO}=\widehat{CKO}=90^0$ (gt)

OB = OC ( cmt )

$\widehat{O_1}=\widehat{O_2}$ (đối đỉnh)

=> ?HOB = ?OC
=> OH = OK ( cạnh tương ứng )
Xét tứ giác BHCK, ta có :
OH = OK ( cmt )
OB = OC ( cmt )
Mà hai đường chéo BC và HK cắt nhau tại O
=> tứ giác BHCK là hình bình hành
=> BH = CK và BK / / CH

3. chứng minh ba điểm M, O, N thẳng hàng.

Xét tứ giác BMCN, ta có :
BM / / CN ( cùng vuông góc AD )
BN / / CM
=> tứ giác BMCN là hình bình hành
=> hai đường chéo BC và NM cắt nhau tại trung điểm mỗi đường
Mà : OB = OC ( cmt )
=> OM = ON
Hay N, O, M thẳng hàng .

4. Chứng minh

Ta có :
BC = AD ( hai đường chéo của hình chữ nhật ABDC )
BE = AD ( gt )
=> BE = BC
=> tam giác EBC cân tại B

=> $\widehat{BCE}=\widehat{BEC}$

Mà : $\widehat{ECN}=\widehat{BEC}$ (so le trong)

=> $\widehat{ECN}=\widehat{BCE}$ (1)

Mặt khác : OD = OC ( O là giao điểm hai đường chéo hình chữ nhật )
=> tam giác COD cân tại O

=> $\widehat{DCB}=\widehat{ADC}$

Mà : $\widehat{ADC}=\widehat{NCA}$ (cùng phụ với góc DAC)

=> $\widehat{ NCA }=\widehat{DCB}$ (2)

Cộng ( 1 ) và ( 2 ), ta được :

$\widehat{ NCA }+\widehat{ECN}=\widehat{DCB}+\widehat{BCE}$

=> $\widehat{ECA}=\widehat{DCE}$

=> CE là tia phân giác góc ACD

=> $\widehat{DCE}=\widehat{ACD} : 2= 45^0$

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

BÀI TẬP RÈN LUYỆN :

BÀI 1 :

Cho tam giác ABC vuông ở C. Gọi M, N lần lượt là trung điểm của BC, AB. Gọi P là điểm đối xứng của M qua N .
a / Chứng minh : Tứ giác MBPA là hình bình hành .
b / Chứng minh : Tứ giác PACM là hình chữ nhật .
c / CN cắt PB ở Q.. Chứng minh BQ = 2 PQ
d / Tam giác ABC có thêm điều kiện kèm theo gì thì hình chữ nhật PACM là hình vuông vắn .

BÀI 2 :

Cho hình bình hành ABCD có M là trung điểm AB và N là trung điểm CD .
a / Chứng minh : tứ giác AMND là hình bình hành .
b / Chứng minh : tứ giác AMCN là hình bình hành .
c / Chứng minh : AC, BD, MN đồng quy .
d / Hình bình hành ABCD có điều kiện kèm theo gì thì tứ giác AMND là hình chữ nhật, hình thoi, hình vuông vắn .

BÀI 3 :

Cho tam giác ABC. Gọi D, E lần lượt là trung điểm của AB và BC .
a. Chứng minh tứ giác ADEC là hình thang
b. Trên tia đối của tia DE lấy điểm F sao cho DF = DE.Chứng minh tứ giác AEBF là hình bình hành .
c. Với điều kiện kèm theo nào của tam giác ABC để AEBF là hình vuông vắn ? .

BÀI 4 :

Cho hình thang cân ABCD ( AB / / CD ). Gọi M, N, P, Q. lần lượt là trung điểm của AB, BC, CD, DA.Biết AC vuông góc BD
a / Chứng minh : Tứ giác MNPQ làhình bình hành .
b / Chứng minh : Tứ giác MNPQ làhình thoi .
c / Nếu AC vuông góc BD thì tứ giác MNPQ là hình gì ? Vì sao ?

BÀI 5 :

Cho DABC vuông tại A, vẽ trung tuyến AM .

Nếu cho AB = 6cm, AC = 8cm. Tính độ dài đoạn thẳng AM.
Gọi D, E lần lượt là trung điểm của AB, AC. Chứng minh tứ giác AEMD.
Gọi F là điểm đối xứng của điểm E qua D. Tứ giác EFBC làhình gì? Chứng minh.
DABC cần có thêm điều điện gì thì AEMDlà hình vuông?

Chia sẻ:

Twitter
Facebook

Thích bài này:

Thích

Xem thêm: Ngày tốt tháng 8 Âm năm 2021: Tháng 8 Âm lịch ngày nào tốt? – https://mix166.vn

Đang tải …

Có liên quan

Source: https://mix166.vn
Category: Hỏi Đáp