Bài tập quy tắc đếm lớp 11 có lời giải – Toán Thầy Định
Mục lục bài viết
I. ÔN TẬP LÝ THUYẾT QUY TẮC ĐẾM
QUY TẮC CỘNG CHO HAI PHƯƠNG ÁN
Giả sử một việc làm V hoàn toàn có thể được triển khai theo giải pháp A hoặc giải pháp B. Có m cách triển khai theo giải pháp A và có n cách triển khai theo giải pháp B, không có cách triển khai nào của giải pháp A trùng với cách triển khai của giải pháp B. Khi đó có m + n cách triển khai việc làm V .
QUY TẮC CỘNG MỞ RỘNG CHO NHIỀU PHƯƠNG ÁN
Bạn đang đọc: Bài tập quy tắc đếm lớp 11 có lời giải – Toán Thầy Định
Giả sử một việc làm V hoàn toàn có thể được thực thi theo một trong k giải pháp A ( 1 ), A ( 2 ), …, A ( k ). Có n ( 1 ) cách triển khai theo giải pháp A ( 1 ), có n ( 2 ) cách thực thi theo giải pháp A ( 2 ), … có n ( k ) cách triển khai theo giải pháp A ( k ), không có cách triển khai nào của những giải pháp trùng nhau. Khi đó có n ( 1 ) + n ( 2 ) + … + n ( k ) cách thực thi việc làm V .
QUY TẮC CỘNG DƯỚI DẠNG TẬP HỢP
Cho A và B là hai tập hợp hữu hạn. Khi đó n ( A ∪ B ) = n ( A ) + n ( B ) – n ( A ∩ B ). Đặc biệt nếu A ∩ B = ∅ thì n ( A ∪ B ) = n ( A ) + n ( B ) .
QUY TẮC NHÂN CHO HAI PHƯƠNG ÁN
Giả sử một việc làm V được thực thi qua hai quy trình liên tục A và B. Có m cách triển khai quy trình A. Với mỗi cách thực thi quy trình A lại có n cách thực thi quy trình B. Khi đó có m. n cách thực thi việc làm V .
QUY TẮC NHÂN MỞ RỘNG CHO NHIỀU PHƯƠNG ÁN
Giả sử một việc làm V được triển khai qua k quy trình liên tục nhau A ( 1 ), A ( 2 ), …, A ( k ). Có n ( 1 ) cách thực thi quy trình A ( 1 ), với mỗi cách thực thi quy trình A ( 1 ) có n ( 2 ) cách triển khai quy trình A ( 2 ), …, với mỗi cách thực thi quy trình A ( k-1 ) có n ( k ) cách thực thi quy trình A ( k ). Khi đó có n ( 1 ). n ( 2 ) …. n ( k ) cách thực thi việc làm V .
QUY TẮC NHÂN DƯỚI DẠNG TẬP HỢP
Tập hợp AxB = { ( x, y ) | x ∈ A, y ∈ B } được gọi là tích Descartes ( Đề-các ) của hai tập hợp A và B .
Khi đó n ( AxB ) = n ( A ). n ( B ) .
II. BÀI TẬP QUY TẮC ĐẾM LỚP 11 CÓ LỜI GIẢI : ĐẾM TRỰC TIẾP
Để đếm số cách triển khai một việc làm, ta phân loại cách triển khai việc làm đó thành những giải pháp, trong mỗi giải pháp lại chia thành những quy trình. Sau đó sử dụng quy tắc nhân và quy tắc cộng để suy ra số cách thực thi việc làm đó .
Bài 1.
Từ những chữ số 1, 2, 3, 4 hoàn toàn có thể lập được bao nhiêu số tự nhiên gồm :
a. Một chữ số .
b. Hai chữ số .
c. Hai chữ số kháu nhau ?
Lời giải :
a. Liệt kê được 4 số thỏa mãn nhu cầu .
b. Gọi số có 2 chữ số cần lập là ab .
Chữ số a có 4 cách chọn, chữ số b có 4 cách chọn
Vậy theo quy tắc nhân ta có : 4.4 = 16 ( số ) .
c. Gọi số có 2 chữ số cần lập là ab .
Chữ số a có 4 cách chọn, chữ số b có 3 cách chọn .
Vậy theo quy tắc nhân ta có : 4.3 = 12 ( số ) .
Bài 2.
Có bao nhiêu số nguyên của tập hợp {1; 2;…; 1000} mà chia hết cho 3 hoặc 5?
Lời giải :
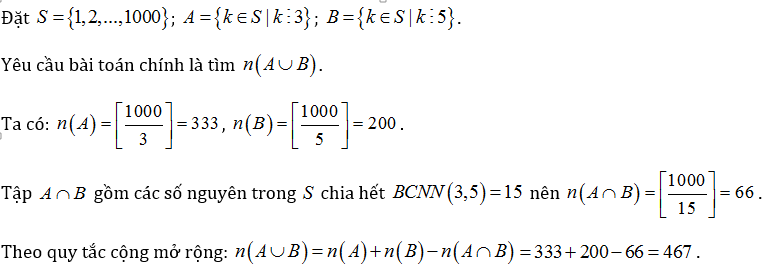
Bài 3.
Có bao nhiêu cách xếp 5 bạn nam và 7 bạn nữ thành một hàng ngang, sao cho không có hai bạn nam nào đứng cạnh nhau .
Lời giải :
Xếp 7 bạn nữ thành hàng ngang có 7.6.5. 4.3.2. 1 = 5040 cách xếp .
Khi đó 7 bạn nữ chia hàng ngang thành 8 khoảng trống .
Xếp 5 bạn nam vào 8 khoảng trống đó sao cho mỗi khoảng chừng trống xếp nhiều nhất một bạn nam. Số cách xếp 5 bạn nam là : 8.7.6. 5.4 = 6720 cách xếp .
Theo quy tắc nhân có : 5040 x 6720 = 33868800 cách xếp .
III. BÀI TẬP QUY TẮC ĐẾM LỚP 11 CÓ LỜI GIẢI : ĐẾM GIÁN TIẾP
Để đếm số cách triển khai một việc làm nào đó, mà việc đếm trực tiếp phức tạp, người ta hoàn toàn có thể sử dụng chiêu thức đếm phần bù. Nghĩa là bỏ đi một giả thiết gây ra sự phức tạp. Khi đó giả sử đếm được m cách thực thi. Trong số cách thực thi đó ta đếm số cách thực thi việc làm mà không thỏa mãn nhu cầu giả thiết bỏ đi được n cách triển khai. Suy ra có m-n cách thực thi việc làm đã cho .
Bài 1.
Trong một hộp có 4 viên bi xanh và 6 viên bi đỏ. Có bao nhiêu cách chọn ra 3 viên bi sao cho có tối thiểu 1 viên bi đỏ ?
Lời giải :
Chọn ngẫu nhiên 3 viên bi bất kể có ( 10.9.8 ) : ( 3.2.1 ) = 120 cách. Số cách chọn 3 viên màu xanh là 4.3.2 = 24 .
Vậy số cách thỏa mãn nhu cầu nhu yếu bài toán là 120 – 24 = 96 cách .
Bài 2.
Trong mặt phẳng có 5 điểm phân biệt A, B, C, D, E. Hỏi có bao nhiêu véc tơ khác véc tơ không. Có điểm đầu và điểm cuối là những điểm A, B, C, D, E thỏa mãn nhu cầu điểm A không phải là điểm đầu ?
Lời giải :
Ta đếm số véc tơ được tạo thành từ 5 điểm là 5.4 = 20 .
Ta đếm số cách chọn véc tơ được tạo thành từ 5 điểm mà điểm A là điểm đầu có 4 véc tơ .
Vậy có 20-4 = 16 véc tơ thỏa mãn nhu cầu .
Bài 3.
Mỗi mật khẩu máy tính gồm 6 ký tự, mỗi ký tự hoặc là một vần âm hoặc là một chữ số và mặt khẩu phải có tối thiểu một chữ số. Hỏi lập được bao nhiêu mật khẩu ?
Lời giải :
Mỗi ký tự có 26 + 10 = 36 cách chọn. Do đó chuỗi gồm 6 ký tự có 36 ^ 6 cách lập .
Số chuỗi 6 ký tự không có chữ số là 26^6 .
Vậy có toàn bộ 36 ^ 6-26 ^ 6 = 1867866560 mật khẩu .
Chúc các bạn học giỏi, thành công!
Tổ hợp xác suất –
Source: https://mix166.vn
Category: Hỏi Đáp











